1591. Shoemaker problem
Shoemaker has n jobs (orders from customers) which he
must make. Shoemaker can work on only one job in each day. For each i-th job, it is known the integer Ti, the time in days it takes
the shoemaker to finish the job. For each day before finishing the i-th job, shoemaker must pay a fine of Si cents. Your task is to
help the shoemaker, writing a program to find the sequence of jobs with minimal
total fine.
Input. Consists of multiple test
cases. The first line of each test case contains the number of jobs n (1 £ n
£ 1000), after which n lines contain the values of Ti (1 £ Ti £ 1000) and Si
(1 £ Si
£ 10000).
Output. For each test case print in
a separate line the sequence of jobs with minimal fine. If multiple solutions
are possible, print the lexicographically first.
|
Sample input |
Sample output |
|
4 3 4 1
1000 2 2 5 5 |
2 1 3
4 |
SOLUTION
greedy
Algorithm analysis
Consider two
jobs with characteristics T1, S1 and T2,
S2.
If the first job
is performed first, and then the second one, the fine is
S1
* T1 + S2 * (T1 + T2)
If the second job is performed
first, and then the first one, the fine is
S2
* T2 + S1 * (T1 + T2)
Consider the condition when
the fine for performing
the jobs in order 1, 2 is
better than when performing the jobs in order 2, 1:
S1
* T1 + S2 * (T1 + T2) < S2
* T2 + S1 * (T1 + T2)
Let's open the
brackets and simplify
the expression:
S2
* T1 < S1 * T2
Or the same as
.
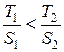Now let we have n jobs. If there
are i-th and j-th jobs for which Ti /
Si > Tj / Sj, then by swapping them in the sequence of execution,
we will reduce the total amount of the fine. Thus, to minimize the fine, the jobs should be
sorted by non-decreasing ratio of the time of their execution to the amount of
the fine.
In case of
equality of the ratio (Ti / Si = Tj / Sj),
the jobs should
be sorted in ascending order of their numbers.
Example
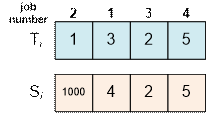
Sort the jobs according to
the non-decreasing ratio of their execution time to the amount of the fine:
We obtain,
respectively, the optimal order of performance of the jobs indicated in
the sample. The third and the fourth jobs have
the same ratio (2/2 = 5/5), so we arrange them in ascending order of job
numbers.
Algorithm realization
Information
about jobs is stored in the
array jobs, which elements are
vectors of length 3. After reading the data, jobs[i][0] contains the execution time of the i-th job Ti,
jobs[i][1] contains the value of the
penalty Si, and jobs[i][2] contains job number i.
vector<int> j(3,0);
vector<vector<int> > jobs;
Sorting function. Comparison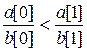 
is equivalent to a[0]
* b[1] < b[0] * a[1]. If the ratios a[0] / b[0] and a[1] / b[1] are the same, then job with a lower
number should follow earlier. Therefore, in this case, it is necessary to
compare the numbers of jobs that are stored in a[2] and b[2].
int
lt(vector<int> a, vector<int> b)
{
if (a[0] *
b[1] == b[0] * a[1]) return a[2] < b[2];
return a[0] *
b[1] < b[0] * a[1];
}
The main part of the program. Read the input data. Fill the array jobs.
while(scanf("%d",&n) == 1)
{
jobs.clear();
for(i = 1; i
<= n; i++)
{
scanf("%d
%d",&j[0],&j[1]); j[2] = i;
jobs.push_back(j);
}
Sort the jobs according to the comparator lt.
sort(jobs.begin(),jobs.end(),lt);
Print the result as
required in the problem statement.
for(i = 0; i < n; i++)
printf("%d ",jobs[i][2]);
printf("\n");
}
Algorithm realization – class
#include <cstdio>
#include <algorithm>
#define MAX 1010
using namespace std;
int
i, n, t, fine, tests;
class
Work
{
public:
int time,
fine, id;
Work (int
time = 0, int fine = 0, int id = 0) :
time(time), fine(fine), id(id) {};
};
Work
*Jobs;
int
f(Work a, Work b)
{
// a.time
b.time
// ------ < ------
// a.fine
b.fine
if (a.time *
b.fine == b.time * a.fine) return a.id <
b.id;
return a.time
* b.fine < b.time * a.fine;
}
int
main(void)
{
while(scanf("%d",&n) == 1)
{
Jobs = new
Work[n];
for(i = 0;
i < n; i++)
{
scanf("%d
%d",&t, &fine);
Jobs[i] = Work(t,fine,i+1);
}
sort(Jobs,Jobs+n,f);
for(i = 0;
i < n; i++)
printf("%d ",Jobs[i].id);
printf("\n");
delete[]
Jobs;
}
}
Java realization
import java.util.*;
class Job
{
int s, t, id;
public Job(int s, int t, int id)
{
this.s = s;
this.t = t;
this.id = id;
}
}
public class Main
{
public static class MyFun implements Comparator<Job>
{
public int
compare(Job a, Job b)
{
if (a.s * b.t == b.s * a.t) return a.id - b.id;
return a.s * b.t - b.s * a.t;
}
}
public static void
main(String[] args)
{
Scanner con = new Scanner(System.in);
while(con.hasNext())
{
int n = con.nextInt();
ArrayList<Job> jobs = new ArrayList<Job>();
for(int i = 1; i <= n; i++)
{
int s = con.nextInt();
int t = con.nextInt();
jobs.add(new Job(s,t,i));
}
Collections.sort(jobs, new MyFun());
for(int i = 0; i < n; i++)
System.out.print(jobs.get(i).id + " ");
System.out.println();
}
con.close();
}
}